활성화 함수(Activation function)란?
딥러닝 모델이나 퍼셉트론과 같은 신경망을 공부하다보면, 활성화 함수(이하 Activation function)라는 단어를 많이 볼 수 있다. 활성화 함수는 layer의 출력을 결정하는 중요한 함수로서, 다양한 종류가 있다. 오늘은 이 활성화 함수의 개념과 그 종류에 대해 알아보겠다.
1. 활성화 함수란?

일반적으로, 활성화 함수는 layer에 입력된 신호에 가중치가 반영된 값을 출력 값으로 변환해주는 함수를 의미한다.
위 그림에서 $x_{1}$과 $x_{2}$라는 입력을 받았을 때, layer의 출력값 $y$는 $f(W_{1}\cdot x_{1} + W_{2}\cdot x_{2})$로 나타낼 수 있다.
이때, 함수 $f()$가 활성화 함수에 해당한다.
예를 들어, 활성화 함수가 임의의 선형 함수라고 가정해보자. $f(x) = 3x+1$일때, $y=3( W_{1}\cdot x_{1} + W_{2}\cdot x_{2})+1$로 계산할 수 있다. $y$를 보면 알겠지만, layer의 출력 결과가 선형 함수임을 알 수 있다.
위 처럼 단순한 네트워크가 아니라, 여러개의 layer가 추가되면 어떨까? 계산이야 복잡해지겠지만, 결과적으로 출력값은 여전히 선형 함수일 것이다. (선형대수때 배운 Additivity와 Homogeneity를 사용하여 증명할 수 있다)
즉, 하고 싶은 말은 활성 함수가 선형이면 비선형성을 절대 구현할 수 없다는 것이다.
그렇다면, 모델이 비선형성을 갖게 하려면 어떻게 해야할까? 답은 바로 비선형성을 가진 활성화 함수를 쓰는 것이다.
이 부분에서 우리는 중요한 2가지 사실을 알아냈다.
- 활성화 함수는 layer의 출력을 결정한다
- 모델이 비선형성을 갖기 위해선 활성화 함수는 비선형 함수여야 한다.
비선형 함수는 정말 많다. 단순히 생각해보면 삼각함수도 비선형 함수고, 지수 함수도 비선형 함수고 log 함수도 비선형 함수인데, 어떤 비선형 함수를 사용해야 모델을 구성할 수 있을까?
2. 대표적인 활성화 함수의 종류
앞서 서술한 것처럼, 비선형 함수는 정말 많다. 하지만, 활성화 함수로서 사용되는 비선형 함수는 대개 다음과 같이 정리할 수 있다.
Step function

입력값이 0이하이면 0을, 그 외에는 1을 반환하는 함수다. 주로 스팸 메일이나, 합격/불합격과 같은 이진 분류 문제에서
사용된다.
Sigmoid function
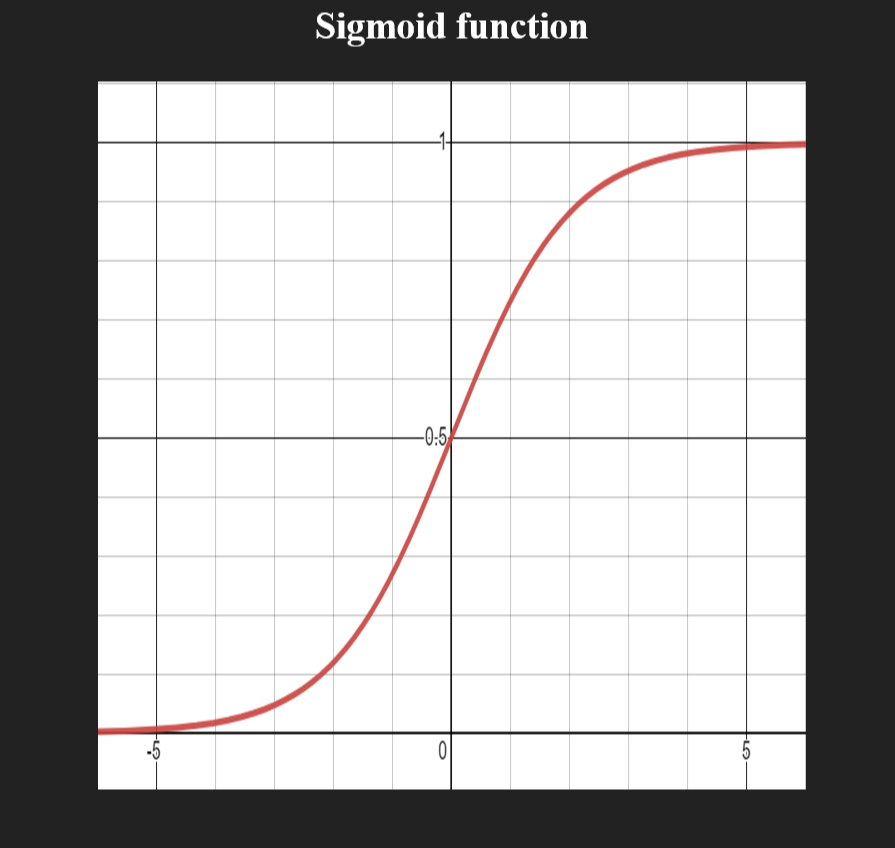
Sigmoid function은 logistic function이라고도 불리며, 주로 이진 분류에서 두 class의 확률을 구하는데 사용된다.
이 함수는 아래와 같이 수식으로 표현할 수 있다.
$$ f(x) = \dfrac{1}{1+{\exp}^{-x}} $$
이 함수의 특징 중 하나는 모든 입력값이 0~1 사이로 mapping 된다는 점인데, 이는 극단적인 값이나 예욋값을 따로 처리할 필요가 없어서 간편하다는 장점도 있다.
Softmax function

Softmax function은 sigmoid의 일반형으로, 3개 이상의 class에 대해 각 class의 확률을 구할때 사용된다.
이 함수를 수식으로 표현하면 아래와 같다.
$$ f(x_j) = \dfrac{\exp^{x_j}}{\sum_{i}{\exp_i}} $$
Sigmoid와 마찬가지로 입력값이 0~1사이로 mapping되며, 각 class에 대한 함숫값의 합은 1이다.
Tanh function

Sigmoid와 비슷하게 생겼지만, 출력값이 -1~1이라는 차이점이 있다. 이러한 특징때문에 평균이 0에 가까워지므로 hidden layer 학습에 조금더 좋은 성능을 보인다.
하지만, Sigmoid와 위 함수 모두 입력값이 아주 크거나 작을 때 함수의 기울기가 0에 가까워진다. 이 경우
경사 하강법을 통한 학습이 매우 느려질 수 있다는 단점이 있다.
ReLU function
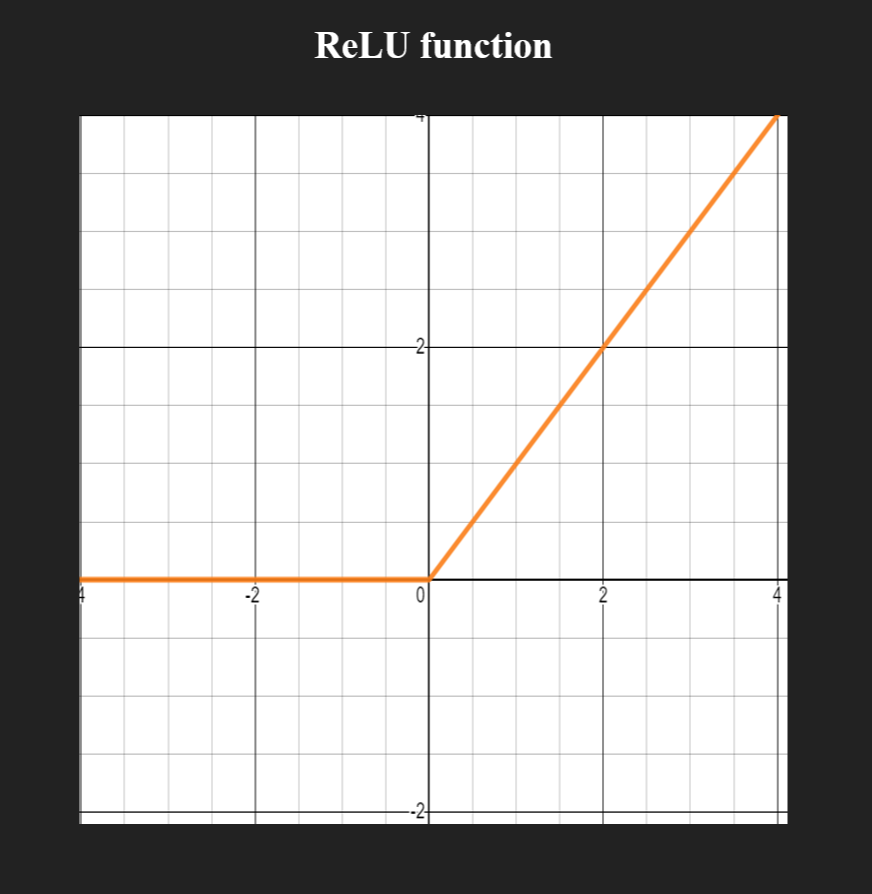
Recified Linear Unit function (ReLU)다. 보통 요즘 모델들의 경우 layer간 활성화 함수로서 ReLU를 많이 사용한다.
그 이유는 단순히 tanh나 Sigmoid와 같은 함수보다 ReLU 함수가 뛰어난 성능을 보이기 때문이다.
ReLU function의 일반적인 수식은 다음과 같다.
$$ f(x) = \max(0, x) $$
실제로 ReLU 함수의 성능을 분석한 논문이 있는데 관심이 있다면 아래의 논문을 참고해보면 좋을 것 같다.
- Review and Comparison of Commonly Used Activation Functions for Deep Neural Networks (Fig. 12):
https://arxiv.org/abs/2010.09458
Review and Comparison of Commonly Used Activation Functions for Deep Neural Networks
The primary neural networks decision-making units are activation functions. Moreover, they evaluate the output of networks neural node; thus, they are essential for the performance of the whole network. Hence, it is critical to choose the most appropriate
arxiv.org
LeLU function

마지막으로 소개할 활성화 함수는 Leaky ReLU function (LeLU)다. ReLU와 거의 비슷하지만 차이점은 입력값이 음수인
부분에서 ReLU처럼 0을 반환하는 것이 아니라는 점이다.
이러한 차이를 둔 이유는 바로 ReLU가 음수 부분에서 기울기가 0이기 때문인데, 이를 해결하기 위해 아주 작은 기울기를
가진 선형함수로 바꾼 것이다.
일부는 LeLU함수가 ReLU보다 성능이 더 좋다고 하는데... 나는 잘 모르겠다.
(ReLU 파트의 링크 건 논문에서만 봐도 LeLU보다 ReLU가 accuracy나 training time적으로 더 좋은 성능을 보인다...)
이로서, 일반적으로 사용하는 대부분의 활성화 함수들에 대해 알아보았다.
3. Summary
오늘 알아본 활성화 함수들에 대해 정리하면 다음과 같다.
- Step function : 0 또는 1을 출력하는 함수로 주로 이진 분류 문제에서 사용된다.
- Sigmoid function : 입력값을 0~1 사이로 압축하고, 극단적으로 크거나 작은 값 및 예욋값을 제거한다.
주로 이진 분류 문제에서 많이 사용한다. - Softmax function : Sigmoid의 일반형으로 3개 이상의 class가 있을 때 분류를 목적으로 사용된다.
- tanh function : 입력값을 -1에서 1 사이로 압축하고, sigmoid 함수보다 더 좋은 성능을 보인다.
- ReLU function : 가장 많이 사용되는 함수로, 입력이 0보다 클 때만 값을 반환한다.
- LeLU function : ReLU 함수의 기울기 문제를 해결한 함수로, 음수 입력값에 대해서도 0이 아닌 기울기를 갖는다.
중요한 것은, task와 model 등 여러 상황을 고려하여 적절한 활성화 함수를 선택하는 것인 것 같다.